(Ce document existe en version pdf)
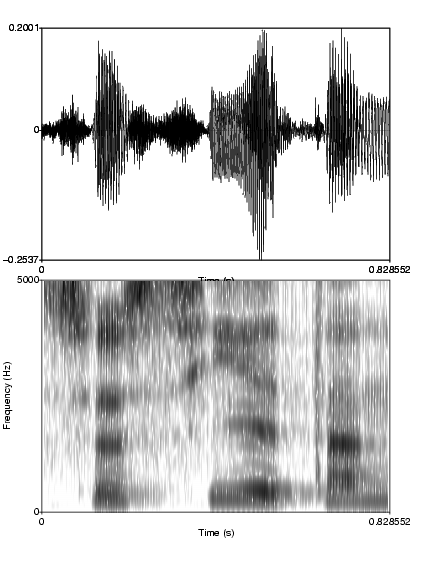
La parole est transmise par un signal acoustique - c'est à dire une onde longitudinale de pression (cf. figure 1) - qui fait vibrer le tympan, mouvement transmis à la cochlée par les os de l'oreille moyenne.

L'intelligibilité de la parole est remaquablement robuste aux distortions du signal acoustique.
Par exemple, le signal de parole utilise essentiellement les fréquences comprises entre 100 et 5000 Hz, mais on peut supprimer une large partie de ces fréquences et le signal demeure compréhensible [Fletcher, 1929]. On peut écréter le signal, voire le discrétiser complétement (remplacant les valeurs positives par +1 et les valeurs négatives par -1) [Licklider, 1946,Licklider, 1950], et il demeure compréhensible.
Quand on interrompt ou qu'on inverse le signal dans des tranches de plusieurs dizaines de millisecondes, la compréhension peut demeurer très bonne Miller and Licklider, [1950,Saberi and Perrot, [1999].
Cela suggère que le signal de parole est très redondant, et aussi, sans doute, que le cerveau « va au delà » des données, c'est à dire interprète un signal incomplet.
L'un des arguments les plus souvent cités en ce sens est le phénomène de restauration phonémique mis en évidence par Warren, [1970] . Il s'agit d'une illusion dans laquelle on entend des sons de parole qui ont en fait été « enlevés » du signal et remplacés par du bruit blanc. Typiquement, les personnes décrivent entendre une phrase intacte avec un bruit superposé.
Le but ce TP est de construire des stimuli et une expérience simple de restauration phonémique similaire à celle décrite dans Samuel, [1981].
Pour créer les stimuli, on va utiliser le logiciel de manipulation de sons Praat développé par Paul Boersma and David Weenink à l'université d'Amsterdam.
L'expérience proprement dite sera programmée dans le language Python avec la librairie pygame.
Note: Utiliser les fonctions Cut/Copy/Paste de la fenêtre
d'édition. Pour créer un bruit blanc: New/Sound/Create Sound,
puis:
formula=randomGauss(0,0.1)
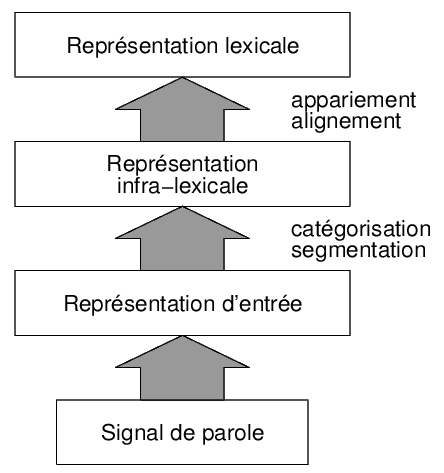
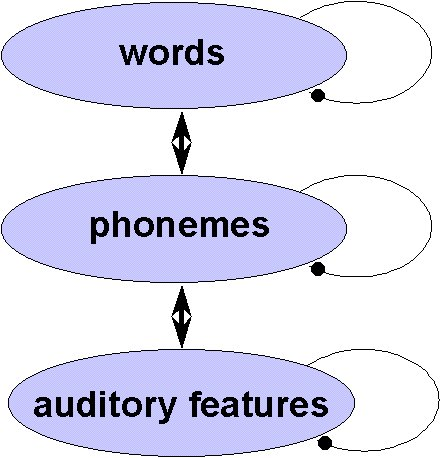
Dans les années 1940, avec les premières techniques d'enregistrement et de visualisation de la parole, il semblait qu'il allait devenir possible de définir des caractéristiques acoustiques invariantes associées à chaque son de parole (les phonèmes). Selon ce point de vue, la perception de la parole consisterait à identifier des patterns acoustiques correspondant, successivement, à chaque phonème. Une fois les phonèmes identifiés, les mots compatibles avec ceux-ci seraient recherché dans le « lexique mental ». Cela correspond à un modèle « montant » (bottom-up) de la perception de la parole (cf. figure 2A). Les grandes distortions qu'on peut imposer au signal de parole suggèrent que s'il existe des invariants, ceux-ci sont assez abstraits.
Des résultats comme ceux de Warren sont généralement interprétés en supposant que la perception est également influencée par les connaissances a priori du sujet. Dans les modèles dits « interactifs » McClelland and Elman, [1986,McClelland and Rumelhart, [1986], cette influence est due à un feed-back des niveaux supérieurs de traitements (lexique, sémantique,...) vers le niveau de décodage en phonèmes (figure 2B).
| A | B |
 |  |
L'expérience originale de Warren (1970) montre-t-elle vraiment qu'il y a une influence des connaissances lexicales sur le décodage des phonèmes ?
Les connaissances des sujets influencent leurs décisions, mais il n'est pas évident qu'elles affectent l'étape précoce de décodage des phonèmes. En d'autres termes, la réponse des sujets pourrait provenir d'un biais de réponse post-perceptuel.
Samuel, [1981] a fait une remarque cruciale : les modèles interactifs prédisent une restauration phonémique plus importante dans des mots que dans des pseudomots, et il a utilisé l'approche de la théorie de détection du signal pour séparer les composantes perceptives et décisionnelles.
La théorie de détection du signal modélise la prise de décision.
Imaginez le scénario suivant: vous écoutez une série d'enregistrements bruités, et vous devez détecter, pour chacun d'entre eux, s'il contient un son cible fixé. Ce son est faible et la détection dans le bruit n'est pas évidente; il y a donc quatre possibilités:
| Décision | ||
| Cible présente | Non | Oui |
| Non | rejet correct | fausse alarme |
| Oui | manqué | détection correcte |
À la fin de l'expérience, il y a donc 4 pourcentages, correspondant à chacune des cases du tableau. En fait, ces 4 pourcentages ne sont pas indépendants2: la performance d'une personne peut être caractérisée, par exemple, par le taux de détection correcte (Hits) et le taux de fausse-alarmes (FA). On peut la représenter par un point dans un repère FA/Hits. Par exemple, la figure 3 montre les performances de 3 sujets (points (a), (b) et (c)). (a) a une performance parfaite ; (c) répond au hasard et (b) répond systématiquement que le signal est présent (son taux de fausse alarme est de 100 %). Bien que les performances de (b) et de (c) soient différentes, on a envie de dire qu'ils ont la même sensibilité de détection (nulle), mais que leur biais de réponse sont différents. 3
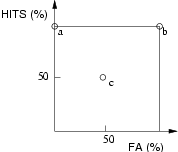
Ces cas sont extrèmes. Grosso-modo, plus la performance d'un sujet est proche du point (a) (ou éloigné de la diagonale principale du carré, d'équation Hits=FA), plus sa sensibilité de détection est bonne. Un sujet non biaisé correspondra à un point situé sur la petite diagonale du carré (Hits=1-FA). La théorie de détection du signal fournit à partir des taux de FA et de Hits, des estimations de la sensibilité et du biais de réponse.
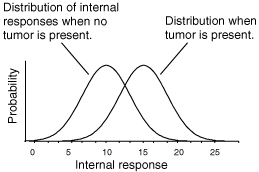
Suivant la théorie de la détection du signal Tanner and Swets, [1954], le traitement perceptif d'un stimulus donne lieu à une réponse interne de l'organisme. La distribution de cette grandeur est différente selon que le stimulus contient la cible ou pas. Par exemple, la figure 4 décrit les distributions provoquées, chez un radiologue, par des clichés de patients ayant ou non des tumeurs. Sa prise de décision est modélisée par un seuil (figure 5)
|
Le calcul de la sensibilité (d') et du biais 'b (dans le
modèle gaussien à variances égales), à partir des taux de fausse alarme
et de hits, est assez simple :
|
|
Où z désigne la fonction inverse de la fonction de distibution de la loi normale. Autrement dit, z transforme un centile dans en ``Z-score''.
|
On peut calculer d' et b avec un tableur : il suffit de trouver la fonction inversant la distribution de la loi normale. Dans OpenOffice Calc, c'est la fonction LOI.NORMALE.STANDARD.INVERSE. Dans Excel, il semblerait que ce soit NORMSINV.
Certains logiciels de statistiques possèdent des fonctions permettant calculer d' et b. Dans le logiciel de statistique ``R'' (http://www.r-project.org), on peut définir les fonctions :
dprime <- function(hit,fa) {
qnorm(hit) - qnorm(fa) }
beta <- function(hit,fa) {
zhr <- qnorm(hit)
zfar <- qnorm(fa)
exp(-zhr*zhr/2+zfar*zfar/2)
}
Votre mission est de programmer une expérience très simple de détection d'un ton pur faiblement audible, caché dans du bruit.
Le sujet entend des stimuli bruités, les uns après les autres dans un ordre aléatoire. Après chaque stimulus, il doit indiquer en cliquant sur un bouton de la souris s'il pense que le stimulus contient un ton pur (c.-à.-d. une sinusoïde) ou non.
Avec Praat, générez un bruit blanc de une seconde, puis 3 autres stimuli durant également une seconde, contenant un ton pur superposé à un bruit blanc. Ajustez les amplitudes de la sinusoïde pour obtenir trois stimuli où le ton pur est difficilement audible (pour que la tâche de détection du ton pur ait un sens). Sauvez ces sons comme des fichiers bruit.wav, son1.wav, son2.wav, son3.wav.
Solution: utiliser New/Sound/Create Sound et une formule du type:
0.1 * sin(2*pi*377*x) + randomGauss(0,0.1)
(Le facteur 0.1 n'est qu'un exemple.)
Voici le code python minimal pour jouer un fichier son:
import pygame.mixer, pygame.time
pygame.mixer.init(22050)
sound=pygame.mixer.Sound('ph1.wav')
channel=sound.play()
while channel.get_busy():
pygame.time.wait(10)
Pouvez-vous compléter ce code pour jouer une série de fichiers sons ?
Voici une possibilité:
import pygame.mixer, pygame.time
pygame.mixer.init(22050)
def play(file):
sound=pygame.mixer.Sound(file)
channel=sound.play()
while channel.get_busy():
pygame.time.wait(10)
liste=['ph1.wav','ph2.wav','ph3.wav','ph4.wav']
while (liste != []):
stimulus = liste[0]
liste = liste[1:]
play(stimulus)
Notez que nous avons défini une fonction play qui joue un fichier son, et une boucle principale qui lit successivement les éléments de la variable liste et appelle la fonction play.
Il ne nous reste plus qu'à aléatoiriser l'ordre des stimuli et à enregistrer les réponses. Essayer de l'implémenter (aide: les deux fonctions utiles sont shuffle et pygame.event.get).
Pour aléatoiriser l'ordre des stimuli, il suffit d'ajouter, après la définition de la variable liste:
import random random.shuffle(liste)
Pour détecter le bouton de souris qui est appuyé après chaque stimulus, on ajoute le code suivant dans la boucle principale :
response = 0
while not(response):
for event in pygame.event.get():
if event.type == MOUSEBUTTONDOWN:
response=event.button
Vous avez maintenant (presque) toutes les pièces du puzzle. Vous pouvez essayer de l'assembler vous-même. Quand ce sera fait, comparer votre résultat au regardez le code du script signal.detection.py. Il y a plusieurs façons de programmer la même chose...
À partir du fichier de résultat, calculer les taux de hits et de fausse alarme (séparement pour son1, son2 et son3), puis calculer d' et b.
Dans l'expérience 2 de Samuel, [1981], les stimuli étaient des mots ou des pseudomots, dont un phonème avait été soit caché par du bruit, soit remplacé par du bruit. À chaque essai, le sujet entendait d'abord le stimulus original, intact, puis une des deux versions modifiées. Il devait dire si le phonème était juste caché ou remplacé par le bruit.
Sélectionner 20 mots français fréquents, bi ou trisyllabiques, contenant un son [f], [s] ou [ch]. (utiliser www.lexique.org)
Inventer 20 pseudomots similaires (mais pas trop ;-).
Enregistrer ces items avec Praat (New/Record mono sound).
Pour chaque item, il faut construire une version où un bruit est ajouté sur le phonème critique, et une version ou le bruit remplace le phonème critique.
Pour additionner un bruit blanc sur un son dans un intervalle temporel, par exemple [0.693,0.776], dans Praat, utiliser Modify/formula:
if x>0.693 and x<0.776 then self[col]+randomGauss(0,0.1) else self[col] endif
Il se pose la question d'avoir un niveau de bruit adéquat (c.-à-d. tel que la tâche de détection ne soit ni trop facile, ni trop difficile). Voir l'article de Samuel (1981) : celui-ci ajuste le niveau de bruit à l'energie moyenne du signal remplacé (root mean square).
Il faudra peut-être piloter pour trouver les amplitudes adéquates.
On pourrait utiliser le programme précédent signal.detection.py. Mais il faudrait construire à priori toutes les paires 'item_intact item_added' et 'item_intact item_replaced'. C'est fastidieux mais possible (et cela peut en fait être automatisé, par exemple dans Praat).
Une autre approche consiste à modifier la boucle principale du programme signal.detection.py pour qu'il joue le fichier intact avant le fichier modifié. Si le nom du fichier intact se déduit facilement du nom du fichier modifié, cette solution est rapide.
Reproduit-on les résultats de Samuel (1981) ?
À propos des effets lexicaux sur la perception des phonèmes, le débat n'est pas clos : voir Norris et al., [2000,Samuel and Pitt, [2003].
Ceux intéressés par la théorie de détection du signal pourront lire Macmillan and Creelman, [2005].
References
1http://www.pallier.org
2Le bombre d'essais contenant la cible ou pas son fixés à l'avance. Par conséquent, la somme de spourcentage sur chaque ligne du tableau fait 100%.
3Remarquons que le biais de réponse peut varier
au cours du temps chez le même sujet.